La cause des paramètres de Planck
Ci-dessus, une image d’artiste représentant messieurs Planck et Einstein.
La longueur de Planck
Le modèle standard détermine la longueur de Planck, par la simple combinaison dimensionnelle des constantes (G ħ c). Cependant il en ignore la cause physique :

La loi DUO5 démystifie cette relation en montrant qu’elle est directement déterminée par les paramètres de l’électron, ex-pôle de Bodys évoluant dans un BEC-fils. Il s’agit du rayon de Compton ƛe et de la masse me de l’électron. Par ailleurs, le temps propre de l’électron est donné par : te = ƛe / c. L’électron a conservé le ratio entre le « point de rebroussement » d’un BEC-fils (ou son rayon) et son « point zéro commun ». Ce ratio vaut strictement ξ² qui est le facteur fondamental de la loi DUO5. On vérifie :

De plus la constante G est directement issue des paramètres de l’électron, selon :
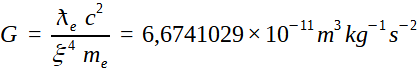
Avec un résultat compatible avec celui recommandé par la CODATA (6.67408(31)×10-11 m3 kg-1 s-2 ). On note que ξ4 représente le nombre de pôles séparés et répartis sur la demi-circonférence du BEC-fossile. Ce surnombre tangentiel ( ξ4 au lieu de ξ3 sur l’axe radial) est responsable de la réduction (facteur ξ) de l’intervalle élémentaire. Cette réduction a déclenché la fusion-séparation-expansion des pôles, devenus électron-positrons. Ce surnombre ξ4 est la cause du ratio entre la force coulombienne et gravitationnelle s’exerçant entre un positron et un électron.
La constante ħ est également issue des paramètres de l’électron, selon :

Ces relations ne sont pas « trouvées incidemment » comme la première, mais découlent de la cohérence globale de la loi DUO5 qui démontre que tout est décliné des Bodys.
La longueur de Planck représente le « point zéro » des 2 pôles liés de l’oscillateur Bodys. C’est également le « point zéro » de l’oscillateur monopolaire « électron » qui n’est autre qu’un pôle causalement séparé de son alter ego. Ce « point zéro » est représenté par le canal 1D du couplage avec un des pôles de Bodys tissant l’espace-temps. C’est ce couplage qui permet la causalité élargie de son état de spin, largement vérifiée par les expériences d’ASPECT relatives à l’intrication des spins.
L’électron a conservé le ratio {amplitude / point zéro} qu’il avait dans son état « pôle de Body ». Ainsi, le ratio ξ2 = {longueur de Compton / longueur de Planck} correspond au ratio {rayon BEC / point zéro commun}.
L’ambiguïté de la masse de Planck
Classiquement la masse de Planck est également donnée par une combinaison dimensionnelle des paramètres G, ħ, c, mais toujours sans en expliquer la cause physique :

Dans laquelle on retrouve le même ratio ξ² avec la masse de l’électron. Cependant la loi DUO5 indique clairement que cette masse n’existe pas. Elle serait celle d’un proton si la mitose (de facteur ξ²) n’avait pas eu lieu, ce qui n’es pas le cas !
Explication : on a vu que les relations classiques de Planck – fonctions de G ħ c – cachent (ou planquent) le lien direct avec l’électron. On a vu que les électrons sont les héritiers des pôles (séparés) de Bodys tissant chaque BEC-fils formant l’espace-temps. Ainsi dans le cadre du BEC-fils, il existe le ratio ξ² entre le rayon du BEC (1021 m) et le rayon du « point zéro commun » (~6 cm). Or les relations de Planck, confondent (sans le savoir) la masse réduite du pôle au « point zéro commun » avec la masse de l’électron (lorsque le pôle est au point de rebroussement). De ce fait, Planck applique la loi M.L = Cte, mais à l’envers ! La véritable masse de Planck, n’est pas ξ² fois plus intense que celle de l’électron mais ξ² fois moins intense ! C’est la « particule de Planck » mpo qui représente la masse réduite d’un pôle positionné au « point zéro commun » d’un BEC-fils.
Masse de Planck réduite ou véritable masse de Planck

Ainsi selon l’application de M.L = Cte, cette masse mPo au « point zéro », augmente jusqu’à celle de l’électron me quand elle arrive au « point de rebroussement » qui est ξ² fois plus étendu. Ainsi, la masse « ponctuelle » de l’électron est en réalité fixée à la longueur de Planck. Sa dualité onde-corpuscule s’exprime entre la longueur de Planck et sa longueur de Compton. Mais son couplage au canal subquantique, confère à sa composante « onde », une extension spatiale largement supérieure, jusqu’au rayon du BEC, sous certaines conditions. La mesure opère ensuite une « réduction du paquet d’ondes » non pas instantanée mais avec le très court délai relatif à la vitesse supraluminique de l’échelle subquantique. C’est la conséquence de son ex-état « pôle de Bodys ».
Planck découvre le Bodys sans le savoir
Le rayon du « point zéro commun » d’un BEC-fils vaut ξ3 fois la longueur de Planck. Le rayon du BEC vaut ξ2 fois le rayon du « point zéro commun ». Il y a donc un ratio ξ5 entre le « point zéro » (longueur de Planck) d’un Bodys seul (synchronisé) et son amplitude relative au rayon du BEC-fossile. Il est inutile de spéculer sur une magique « inflation cosmique ». Il suffit de considérer la vitesse subquantique du pôle émis du « point zéro commun » et son ralentissement à la vitesse c, quand il arrive au rayon du BEC-fossile.
Comme le rayon du « point zéro commun » d’un BEC-fils, est ξ3 fois plus grand que la longueur de Planck, son volume contient ξ9 particules de Planck séparées par la longueur de Planck. Cela revient à ξ3 couches de ξ6 particules chacune. C’est la configuration du BEC-fils (issu de la mitose) mais avec des intervalles se dilatant jusqu’à ξ fois pour arriver à la longueur de Compton. Ainsi le BEC a en permanence ξ3 couches de pôles oscillants dont ξ couches sont toujours présentes dans le « point zéro commun ». L’intervalle isotrope et élémentaire des ξ2 couches extérieures, varient de la longueur de Planck à la longueur de Compton de l’électron, selon la loi canonique M.L = Cte.
Le temps et la vitesse de Planck
Comme pour les autres paramètres de Planck, le modèle standard ignore la cause de cet intervalle temporel ultra-court, ξ2 fois inférieur au temps de l’électron. La loi DUO5 indique que la fréquence de l’électron est héritée du Bodys. Cela correspond au temps : te = ƛe / c. Cela veut dire qu’en sortie du « point zéro commun », l’intervalle temporel est calibré au temps de Planck qui permet d’émettre ξ2 couches dans le temps te = ƛe / c . Ainsi le le temps de Planck est le temps relatif au « point zéro commun » du BEC, soit le temps de l’électron divisé par ξ2.

En prenant naïvement le ratio : longueur de Planck / temps de Planck, on obtient la vitesse c. Mais la vitesse de Planck ne s’inscrit que dans le cadre élargi du BEC-fils. Elle est maximale à la sortie du « point zéro commun ». Elle permet de parcourir le rayon du BEC qui est ξ2 fois plus vaste que le rayon du « point zéro commun » à la fréquence de l’électron. Ainsi elle vaut ξ2 fois la vitesse c. C’est cette vitesse subquantique qui explique l’énigme de la causalité élargie (ou non locale) relative aux spins intriqués. Ainsi la vitesse maximale subquantique, est donnée par :

et pour la première fois, la vitesse quantique, c = 2.998456×108 m/s est déterminée ci-après, avec les paramètres G ħ, eux-mêmes déclinés des paramètres de l’électron :

Cette relation vient confirmer une fois encore, l’implication du rayon de Compton de l’électron ƛe et le fameux facteur ξn qui régit tout l’univers.
Conclusion
La vitesse subquantique des pôles de Bodys varie de c0 au point zéro commun à c, au point de rebroussement. Tant que l’intervalle critique n’est pas atteint, le rebroussement s’effectue et les cycles se poursuivent. Mais lors de la « saturation-fusion-masquage des charges », les pôles sont libérés de leur Bodys respectif. Ainsi, la somme des pôles libérés, forment la matière en expansion à vitesse initiale c. Mais la mitose en 5 phases, implique une expansion en couches de vitesses de 0 à 5 c qui donnent l’illusion que chaque point du cosmos en est le centre. Non le centre est le BEC-fossile qui est d’ailleurs largement visible (on note l’appellation « point » pour minimiser sa taille de plus d’un milliard d’années-lumière), du côté de l’Eridan. La mystérieuse et opportune « inflation cosmique » du modèle standard, est juste l’action subquantique des Bodys qui fait passer la vitesse de c0 à c. Les équations dimensionnelles de Max Planck ont appliqué (sans le savoir) la loi canonique M.L = Cte. Mais concernant la masse, cette loi doit tenir compte non pas de la masse de l’électron qui évoluerait vers la forte masse de Planck, mais de la masse réduite d’un pôle évoluant vers la masse de l’électron (et du positron à parité égale). La grande erreur du modèle standard est de croire à l’universalité de l’expérience locale. Cela se traduit donc par le rejet arbitraire du statut initial de l’électron qui est un boson comme son ancêtre, le Bodys. La création locale d’une paire électron-positron lui confère le statut de fermion. En énonçant le « principe cosmologique » (spéculant une homogénéité et une isotropie de l’univers), les « pères » du modèle standard sont tombés dans le piège du simplisme. Malgré le désaccord flagrant amené par plusieurs mesures cosmiques récentes, les inconditionnels du modèle standard, continuent de « croire » en la toute puissance des « pères » de l’école de Copenhague.
Tous mes articles
3 réponses
[…] Commun (PZC) du BEC. A ce point zéro la « masse-image » de l’électron est celle de Planck réduite mPo. Le couplage de l’électron à la non-localité subquantique des Bodys, est la cause de […]
[…] longueur de Compton et l’épaisseur 1D du Bodys avec lequel il est couplé. Conformément aux contraintes DUO5, cette épaisseur est fixée à la longueur de Planck. Ce changement conjoint de taille et de […]
[…] loi héritée est à la source de la constante de Planck […]